How to Find Continuity the Increasing and Decreasing of a Function
Increasing and Decreasing Functions
Introduction to Increasing and Decreasing Functions
Increasing and Decreasing function is one of the applications of derivatives. Derivatives are used to identify that the function is increasing or decreasing in a particular interval.
Generally, we know that if something is increasing, it is going upward and if something is decreasing it is going downwards. Hence if we talk graphically, if the graph of function is going upward then it is an increasing function and if the graph is going downward then it is a decreasing function.
Increasing and Decreasing Function

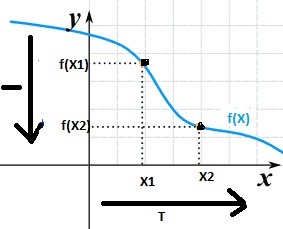
A function is said to be an increasing function if the value of y increases with the increase in x. As we can see from the above figure that at the right of the origin, the curve is going upward as we are going to the right so it is called Increasing Function.
A function is said to be a decreasing function if the value of y decreases with the increase in x. As above, in the left of the origin, the curve is going downward if we are moving from left to right.
Definition of Increasing Function
This is the definition of a function which is increasing on an interval.
If there is a function y = f(x)
- A function is increasing over an interval, if for every x1 and x2 in the interval,
x1 < x2, f( x1) ≤ f(x2)

-
A function is strictly increasing over an interval, if for every x1 and x2 in the interval,
x1 < x2, f( x1) < f(x2)
There is a difference of symbol in both the above increasing functions.
Definition of Decreasing Function
If there is a function y = f(x)
-
A function is decreasing over an interval , if for every x1 and x2 in the interval,
x1 < x2, f( x1) ≥ f(x2)
-
A function is strictly decreasing over an interval, if for every x1 and x2 in the interval,
x1 < x2, f( x1) > f(x2)
There is a difference of symbol in both the above decreasing functions.
Definition of Increasing and Decreasing function at a point
Let x0 be a point on the curve of a real valued function f. Then f is said to be increasing, strictly increasing, decreasing or strictly decreasing at x0, if there exists an open interval I containing x0 such that f is increasing, strictly increasing, decreasing or strictly decreasing, respectively in I.
If there is a function f and interval I = (x0 – h, x0 + h), h > 0
-
It is said to be increasing at x0 if f is increasing in (xo - h, x0 + h)
x1 < x2 in I ⇒ f(x1) ≤ f(x2)
-
It is said to be strictly increasing at x0 if f is strictly increasing in (x0 - h, x0 + h)
x1 < x2 in I ⇒ f(x1) < f(x2)
-
It is said to be decreasing at x0 if f is decreasing in (xo - h, x0 + h)
x1 < x2 in I ⇒ f(x1) ≥ f(x2)
-
It is said to be strictly decreasing at x0 if f is strictly decreasing in (x0 - h, x0 + h)
x1 < x2 in I ⇒ f(x1) > f(x2)

How derivatives are used to find whether the function is Increasing or Decreasing Function?
We can use the first derivative test to check whether the function is increasing or decreasing.
Theorem
Let f be continuous on [a, b] and differentiable on the open interval (a, b). Then
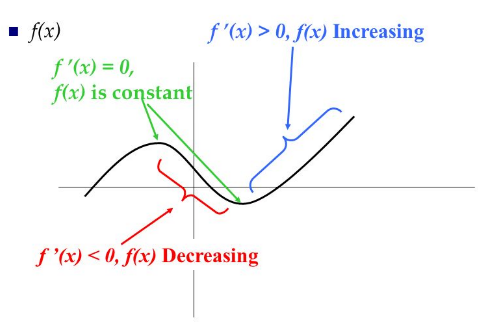
(a) If f′(x) > 0 for each x ∈ (a, b) then f is increasing in interval [a, b]
(b) If f′(x) < 0 for each x ∈ (a, b) then f is decreasing in interval [a, b]
(c) If f′(x) = 0 for each x ∈ (a, b) then f is a constant function in [a, b]
This can be proved with the help of mean value theorem.
Proof:
Let x1, x2 ∈ [a, b] such that x1 < x2
Now we can prove it with the help of Mean value theorem, which says that there is a point c between x1 and x2 so that
Let x1, x2 ∈ [a, b] such that x1 < x2
Now we can prove it with the help of Mean value theorem, which says that there is a point c between x1 and x2 so that

a. Let fꞌ(c) ≥ 0

Hence, f is an increasing function.
b. Let fꞌ(c) ≤ 0

Hence, f is a decreasing function.
c. Let fꞌ(c) = 0

Hence, f is a constant function.

| 1. f is strictly increasing in (a, b) if f ' (x) > 0, ∀ x ∈ [a, b] |
| 2. f is strictly decreasing in (a, b) if f ' (x) < 0, ∀ x ∈ [a, b] |
| 3. f is increasing or decreasing on R if it is increasing or decreasing in every interval of R |
What is constant function?
Constant function is a horizontal line.

As we know that the derivative is zero and y is always 4 in the above figure. This is the graph of line with one variable.
If we talk about curve, the function will be constant if its fꞌ(c) = 0.

Here in the above figure, at green points the curve is neither increasing nor decreasing. The slope of the curve is zero at these points. It could be the highest or the lowest point of the curve in its neighborhood.
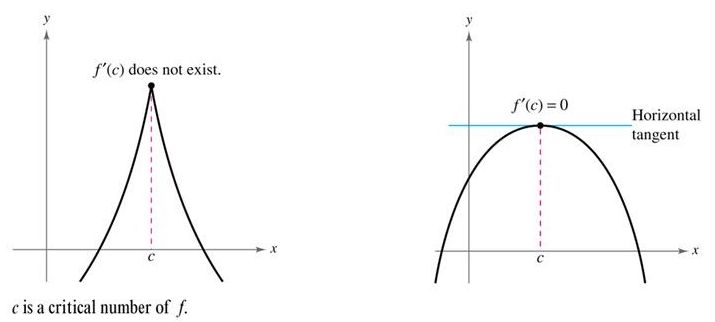
Definition of Critical Numbers
The Critical Numbers for a function f are those numbers c in the domain of f for which fꞌ(c) = 0 or does not exists.
A critical point is a point whose x coordinate is the critical number c and the y coordinate is the f(c).
What are intervals of increase and decrease?
Interval is basically all the numbers between given two numbers.
If we talk about curve, we can say the portion of curve which is coming in between the two given numbers on the x-axis is the required interval.

As in the above figure,
Interval | Type of function |
| (-5,-2) | Increasing |
| (-2,1) | Constant |
| (1,3) | Increasing |
| (3,5) | decreasing |
Calculation of intervals of increase or decrease
To calculate the intervals of increase or decrease function, we need to follow some steps:
-
First of all, we have to differentiate the given function.
-
Then solve the first derivative as equation to find the value of x.
-
The first derivative: f'(x) = 0.
-
-
Form open intervals with the values of the x which we got after solving the first derivative and the points of discontinuity.
-
Take a value from every interval and find the sign they have in the first derivative.
-
If f'(x) > 0 is increasing.
-
If f'(x) < 0 is decreasing.
-
-
Write the intervals of increase and decrease:
Examples of Increasing and Decreasing Functions
Example 1:
Find the intervals of increase and decrease of the function f(x) = x3 − 3x + 2.
Solution:
f(x) = x3 − 3x + 2.
Find the derivative of f(x)
f'(x) = 3x2 −3
Solve the derivative as f'(x) = 0
 3x2 −3 = 0
3x2 −3 = 0
3x2= 3
x2 = 1
x = -1 and x = 1
Now we have to check the sign of first derivative in every interval to find the function is increasing or decreasing.
-
On the interval (−∞, −1),
Let x = −2
f'(−2) = 3(−2)2 −3
f'(−2) = 12 −3
f'(−2) = 9 > 0
-
On the interval (−1, 1),
Let x = 0
f'(0) = 3(0)2 −3
f'(0) = −3 < 0
-
On the interval (1, ∞),
 Let x = 2
Let x = 2
f'(2) = 3(2)2 −3
f'(2) = 12 −3
f'(2) = 9 > 0
Hence,
The function is Increasing in the intervals: (−∞, −1) and (1, ∞)
The function is decreasing in the interval: (−1, 1)
Example 2:
Find the intervals in which the function f(x) = 2x3 – 3x2 -36x +7 is
-
Strictly Increasing
-
Strictly Decreasing.
Solution:
A function is strictly increasing or decreasing on an open interval where its derivative is positive or negative.
Given:
f(x) = 2x3 – 3x2 -36x +7
The derivative of f(x) will be
fꞌ(x) = 6x2 – 6x -36
= 6(x2 – x -6)
= 6(x2 – 3x + 2x – 6)
= 6[x(x – 3) + 2(x – 3)]
= 6[(x + 2) (x – 3)]
Now we know that fꞌ(x) = 0
So x = -2, 3
Now -2 and 3 are dividing the number line in the three disjoint intervals
(-∞,-2)
(-2, 3)
(3, ∞)
Now we have to check the sign of first derivative in every interval to find the function is increasing or decreasing.
-
On the interval (−∞, −2),
Let x = −3
f'(−3) = 6[(x + 2) (x – 3)]
f'(−3) = 6[(- 3 + 2) (- 3 – 3)]
f'(−3) = 6[(-1) (- 6)]
= 6(6)
= 36 > 0
-
On the interval (−2, 3),
Let x = 0
f'(0) = 6[(0 + 2) (0 – 3)]
f'(0) = 6( – 6)
= – 36 < 0
-
On the interval (3, ∞),
Let x = 4
f'(4) = 6[(4 + 2) (4 – 3)]
f'(4) = 6[6.1]
= 36 > 0
Hence,
The function is strictly Increasing in the intervals: (−∞, −2) and (3, ∞)
The function is strictly decreasing in the interval: (−2, 3)
More Readings
Increasing and Decreasing Functions
Source: https://www.askiitians.com/iit-jee-applications-of-derivatives/increasing-and-decreasing-functions/
0 Response to "How to Find Continuity the Increasing and Decreasing of a Function"
Post a Comment